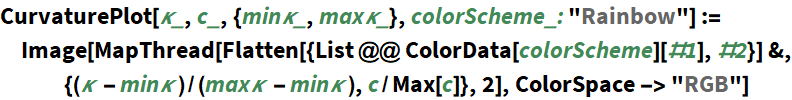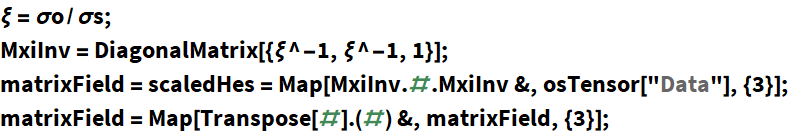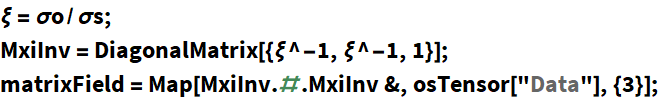LIE ANALYSIS TUTORIAL

Step By Step Gauge Frames SE(2)

Step by Step GuidePlotting the Exponential Curves
Short Implementation

In this tutorial we show how you can compute a data-adaptive (Gauge-)frame. First we show a step by step procedure for two different methods, then we show a short implementation that makes optimal use of the Lie Analysis package.

OrientationScoreGaugeFrames[ObjPositionOrientationData, {σs,σo}, options]computes the data-adaptive frame from the ObjPositionOrientationData using the Gaussian scales σs and σo
OrientationScoreTensor[ObjPositionOrientationData, {σs,σo},derivativeIndex]computes the Hessian or structure tensor from the ObjPositionOrientationData

Functions for the data-adaptive frame.

Load package and some general functions and variables
In[1]:=
Click for copyable input
In[2]:=
Click for copyable input
Out[2]=
In[3]:=
Click for copyable input

Step by Step Guide

Method 1: Symmetric Product Hessian

Step 1: Compute orientation score
Click for copyable input
Step 2: Compute Hessian from orientation score
Click for copyable input
Step 3: Symmetrize the Hessian and make it dimensionless
Click for copyable input
Step 4: Apply external regularization (smoothing the matrix field)
Click for copyable input
Step 4: Compute eigenvectors
Click for copyable input
Step 5: Compute curvature
Click for copyable input
Step 5: Compute orientation confidence
Click for copyable input
Show result
Click for copyable input

Method 2: Structure Tensor

Step 1: Compute orientation score
Click for copyable input
Step 2: Compute Structure Tensor from orientation score
Click for copyable input
Step 3: Symmetrize the Hessian and make it dimensionless
Click for copyable input
Step 4: Apply external regularization (smoothing the matrix field)
Click for copyable input
Step 4: Compute eigenvectors
Click for copyable input
Step 5: Compute curvature
Click for copyable input
Show result
Click for copyable input

Short Implementation

A minimal Lie Analysis setup
Click for copyable input
Click for copyable input
Click for copyable input

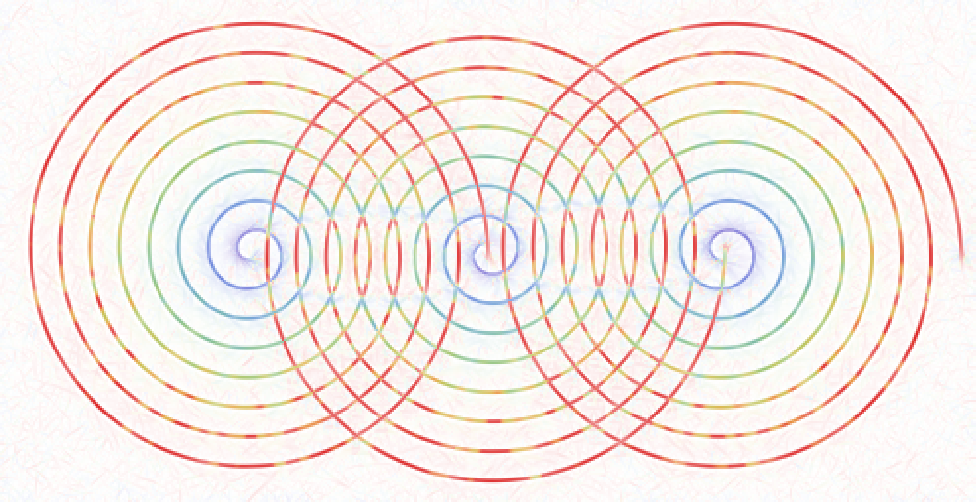
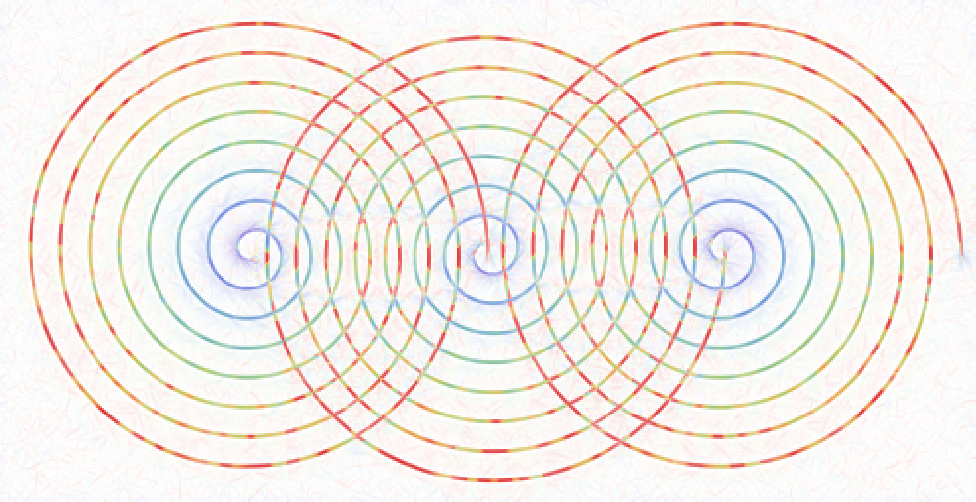
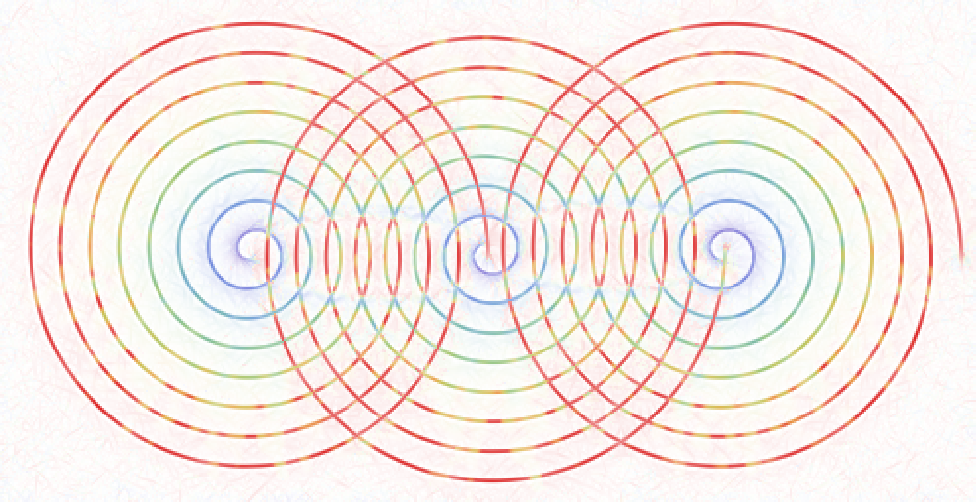
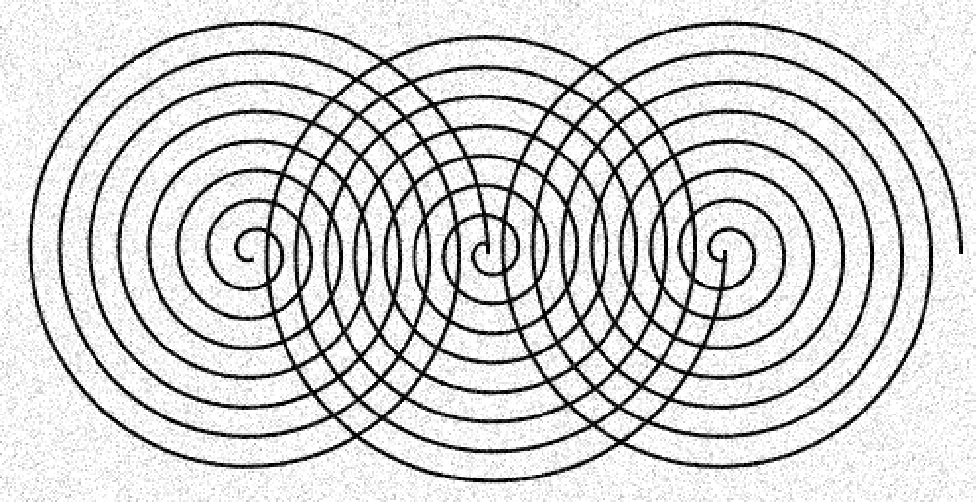
Plotting the Exponential Curves

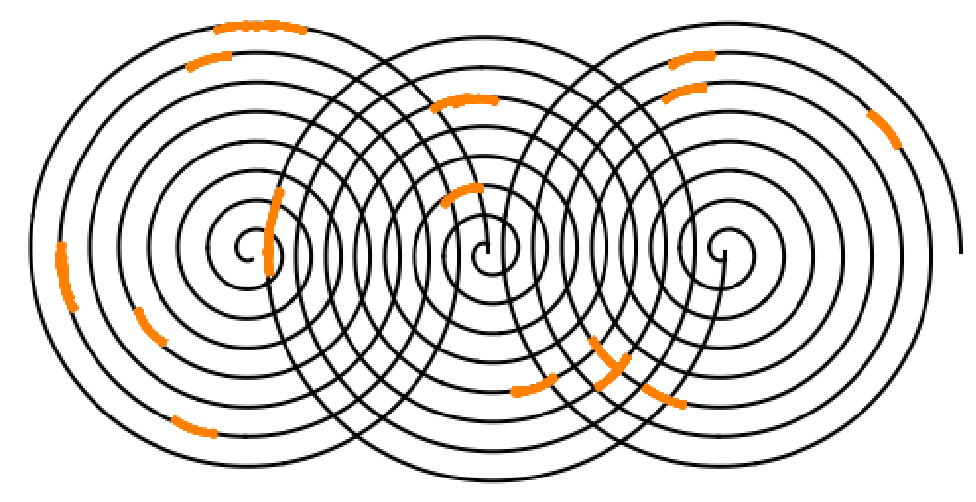
Functions for the group product and exponential map
Click for copyable input
Function for extracting the group element that maximizes the absolute value of the orientation score (optimal θ for each x,y)
Click for copyable input
Extract the group elements and tangent vectors
Click for copyable input
Click for copyable input
Plot the results (projected to the xy plane)
Click for copyable input
  • Fast Marching
  • Processing on 2D Images
  • Working With Objects