Processing on 3D Images
| CakeWaveletStack3D | constructs a ObjCakeWavelet3D which can be used by OrientationScoreTransform to construct an orientation score |
| OrientationScoreTransform3D | constructs an Obj3DPositionOrientationData which represents an orientation score using an ObjOrientationWavelet3D |
| InverseOrientationScoreTransform3D | applies reconstruction to Obj3DPositionOrientationData |
| LeftInvariantDerivatives3D | computes the left-invariant derivatives from Obj3DPositionOrientationData |
| OrientationScoreGaugeFrames3D | computes a data-adaptive frame from Obj3DPositionOrientationData |
| FastMarching | computes the shortest path between seeds and tips |
| GlyphPlot | visualization of the Obj3DPositionOrientationData |
Functions which can be used in 3d image processing.
| In[1]:= |
Orientation Scores
An orientation score Uf of a function f can be constructed by means of convolution with some anisotropic filter ψ. There is much common ground between the Orientation Scores in 2D and 3D, however implementations differ quite much as the complexity of Orientation Scores from 3D images is much higher. Therefor the functions that work with Orientation Scores from 3D images have a post-fix 3D.
Orientation Sensitive Wavelets: Cake Wavelets
| CakeWaveletStack3D[OrientationSpecification, waveletSize, options] | constructs a ObjCakeWavelet3D stack for 3D images using the orientationSpecification; which can be a Integer value indicating the number of orientations, a list of unit vectors or an ObjSphereSampling. |
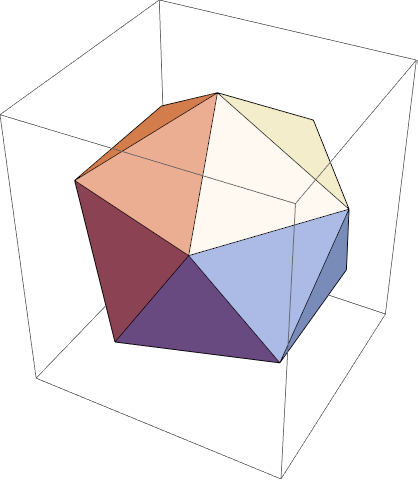
Cake wavelets are, just as in the 2D case, designed in the Fourier domain. Obviously in the 3D case the Fourier space is also 3D, thus instead of a circle we are now dealing with a sphere limited Fourier domain. A cake wavelet stack for 3D images can be created using the function CakeWaveletStack3D.
To see all parameters that model the shape of the wavelets, please take a look at the options section in CakeWaveletStack3D to see their influence on the shape. The parameters are summarized bellow.
option name | default value | |
| "Epsilon" | Automatic | the option Epsilon determines which orderLmaxspherical harmonics is used |
| "SigmaAngle" | False | controls the angular width |
| "Gamma" | N | specifies the distance between the Nyquist frequency and the inflection point |
| "DcStandardDeviation" | 3 | low frequency filter σ |
Parameters to control the shape of the wavelets.
By default the used orientations are computed using an electrostatic model with a random initialization step. Therefor each time you compute the wavelets a different set of orientations is used. This might be inconvenient, especially if you want to compare. Therefor it is also possible to provide a list of orientations as a unit vectors. For example we could use tessellations to compute our orientation vectors.
Another method to input the orientation is by using a ObjSphereSampling which can be constructed using a common function (see Common Functions).
Note that OrientationScoreTransform3D uses these cake wavelets by default internally.
Construction
Construction of an orientation score is convolution of an image f, with the anisotropic wavelet ψ. The function OrientationScoreTransform can be used to do this. The function can be used in different ways.
| OrientationScoreTransform3D[image, options] | constructs an Obj3DPositionOrientationData from image using the parameters specified by the options |
| OrientationScoreTransform3D[image,ObjOrientationWavelet] | constructs an Obj3DPositionOrientationData from image using the supplied ObjOrientationWavelet |
Functions to construct orientation scores from a 3-dimensional image.
Simple Usage
To construct an Orientation Score, only the image needs to be provided to OrientationScoreTransform3D. Lets load an example image from the LieAnalysis server using the function LieAnalysisData. Please note that you need an internet connection for this or have loaded the image before.
The default wavelet is used to construct these orientation scores. To see the used wavelets, you can request the element "Wavelets" from the Obj3DPositionOrientationData, which returns an ObjOrientationWavelet.
Options
The shape of the wavelets can be controlled using the options of OrientationScoreTransform3D. The following table shows the available options.
option name | default value | |
| "Orientations" | 12 | number of orientations or list of orientations |
| "WaveletSize" | 11 | dimensions of the wavelets |
| "Epsilon" | Automatic | the option Epsilon determines which orderLmaxspherical harmonics is used |
| "SigmaAngle" | False | controls the angular width |
| "Gamma" | N | specifies the distance between the Nyquist frequency and the inflection point |
| "DcStandardDeviation" | 3 | low frequency filter σ |
Table containing the options that can be specified for OrientationScoreTransform3D.
Sometimes it is required that we resample the orientations of an Obj3DPositionOrientationData, for this purpose a Lie Analysis common function (see Common Functions) ResampleOrientations can be used. This makes use of the ObjSphereSampling. Please note that the resampling of the orientation axis is done through Spherical Harmonics and therefore loss off precision needs to be taken into account (especially if you come from a low number of orientations).
Precomputed Wavelets
Another way to use the OrientationScoreTransform3D is to precompute the wavelets, so that you can use them in multiple transforms. It is also recommended for speed if the same wavelets are used for different datasets.
Reconstruction
You might want to apply reconstruction to construct an image from your Orientation Scores. For example when you have enhanced image in the Orientation Score domain and want to go back to your spatial domain.
| InverseOrientationScoreTransform3D[Obj3DPositionOrientationData, options] | Applies reconstruction to Obj3DPositionOrientationData by using the specified options |
Compute the inverse from the OrientationScoreTransform.
The default inverse transform is executed by integrating the orientation axes using the function InverseOrientationScoreTransform.
Reconstruction without low frequencies
The low frequencies have been removed from the transform (controlled by the parameter "DcStandardDeviation") and saved in a separate volume (see Obj3DPositionOrientationData). Thus the center of the Cake in the Fourier domain has been taken out. By default these low frequencies are used by the reconstruction. Sometimes it is not appropriate to do this as the Orientation Score might have been scaled or you just don't want to use them. In this case you can specify the option "UseDcComponent" and set it to False.
Reconstruction methods
Different methods for reconstruction can be used. The default reconstruction method is simply integrating over the orientation dimensions (summation). Besides summation, both exact and L2-norm preserve reconstruction can be used by specifying the option "Method".
Visualization
| GlyphPlot | creates a glyph visualization from Obj3DPositionOrientationData |
Visualization options for Obj3DPositionOrientationData.
Left-Invariant Derivatives
The function OrientationScoreDerivatives3D allow to compute Gaussian derivatives with respect to the left-invariant frame.
| LeftInvariantDerivatives3D[Obj3DPositionOrientationData, {σs,σo},derivativesIndex] | computes the left-invariant derivative AderivativeIndex from Obj3DPositionOrientationData using the specified σs and σo. |
| LeftInvariantDerivatives3D[Obj3DPositionOrientationData, {σs,σo}, {derivativeIndex..}] | computes a list of left-invariant derivatives |
| LeftInvariantDerivatives3D[Obj3DPositionOrientationData, derivativeSpecification] | computes the left-invariant derivativeSpecification from Obj3DPositionOrientationData using a finite differences method |
| OrientationScoreTensor3D[Obj3DPositionOrientationData,{σs,σo},derivativesSpecification] | computes a left-invariant derivativeSpecification tensor from Obj3DPositionOrientationData using σs and σo |
| OrientationScoreTensor3D[Obj3DPositionOrientationData,derivativesSpecification] | computes a left-invariant derivativeSpecification tensor from Obj3DPositionOrientationData using a finite differences method |
Computation of derivatives in the left-invariant frame.
Now we can compute the left-invariant Gaussian derivatives by supplying the Obj3DPositionOrientationData, Gaussian scales and obviously in which direction we would like to compute the derivative. The directions are indicated by the indices (i) of the left invariant frame (Ai). For example if we would like to compute the A3 derivative (in the direction of the structures in the orientation scores)
Instead of the Gaussian derivatives also a finite difference method can be used to compute the left-invariant derivatives. Simply do not specify any scales to the LeftInvariantDerivatives3D and OrientationScoreTensor3D and the finite differences method is used instead of the Gaussian derivatives method.
In the 2D case it was possible to compute derivatives up to any order, in the 3D case this is limited to second order derivatives. It is also possible to compute multiple derivatives at once. Therefore instead of supplying a single integer, a list of integers can be supplied.
The output of the function might not what you would expect. In some cases it is more useful to have the derivatives as the last dimension of you Data element (e.g. in the case of a gradient or hessian). To this purpose the OrientationScoreTensor3D function can be used.
There are two predefined Tensors, the Hessian and gradient, you can use these by supplying a string instead of a list of integers.
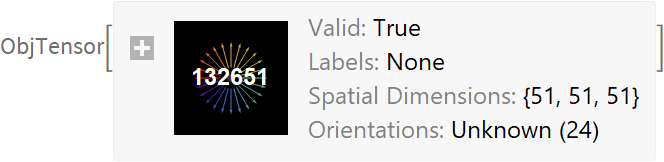
It is also possible to convert a list of Obj3DPositionOrientationData to a single ObjTensor. Simply supply the list of Obj3DPositionOrientationData to the OrientationScoreTensor3D. Note that the element "Labels" is not longer available as these are unknown.
Locally Adaptive Frame
| OrientationScoreGaugeFrames3D | construct a data adaptive frame from an Obj3DPositionOrientationData |
Fast Marching (Windows only)
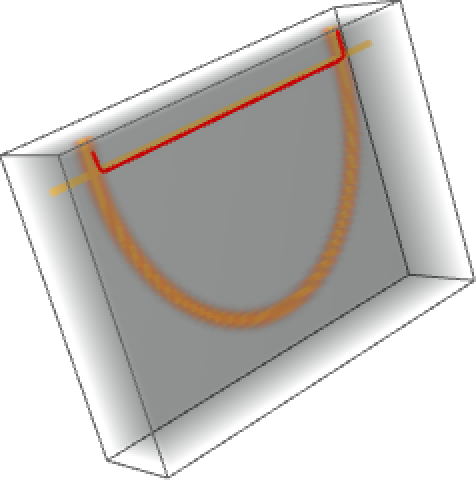
| FastMarching[costFunction,seeds,tips] | returns a ObjFastMarchingResult which contains the shortest path between seeds and tips using the costFunction |